Heat, Internal Energy and Work

An ideal is filled in a closed, rigid and thermally-insulated container. A coil of $100\mathrm{\Omega }$ resistance and carrying a current of $1 \mathrm{A}$ supplies heaT to the gas. The change in the internal energy of the gas after $5$ minutes will be:

For an ideal gas, its internal energy is the function of its:

A gas expands from a volume of $1 {\mathrm{m}}^3$ to a volume of $2 {\mathrm{m}}^3$ against an external pressure of ${10}^5 \mathrm{N} {\mathrm{m}}^{-2}$. The work done by the gas will be

Calculate the magnitude of work done (in joules) when $0.2$ mole of an ideal gas at $300 \mathrm{K}$ expands isothermally and reversibly from an initial volume of $2.5$ litres to the final volume of $25$ litres.

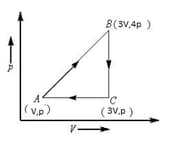
Calculate the work done by an ideal gas in the thermodynamic process $ABCD$ depicted in the adjoining $P-V$ graph.

An insulated container containing ideal monoatomic gas of molar mass $m$ is moving with a velocity $v_0$. If the container is suddenly stopped. The change in temperature is

For the reaction (at $1240 \mathrm{K}$ and$1$atm.)

$\mathrm{C}\mathrm{a}\mathrm{C}{\mathrm{O}}_3\left(s\right)\to \mathrm{C}\mathrm{a}\mathrm{O}\left(s\right)+\mathrm{C}{\mathrm{O}}_2\left(\mathrm{g}\right)$

$∆\mathrm{H}=176$ kJ/mol; $∆\mathrm{E}$ will be

Internal energy is sum of

If gas expands at constant temperature and pressure, then its

The percentage change in internal energy, when a gas is cooled from $\mathrm{927 }°\mathrm{C}$ to $\mathrm{27 }°\mathrm{C}$, is

Among the following gases, the one which possesses the largest internal energy is

Which one of the following statements is true, in respect of the usual quantities represented by $∆Q, ∆U$ and $∆\mathrm{W.}$

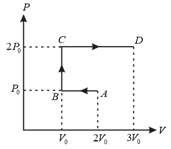
A sample of ideal monoatomic gas is taken around the cycle, $ABCA$ as shown in the figure. The work done during the cycle is

Calculate the specific heat capacity C_v of a gaseous mixture consisting of v₁ moles of a gas of adiabatic exponent ${\gamma }_1$ and ${\text{v}}_2$ moles of another gas of adiabatic exponent ${\gamma }_2$.

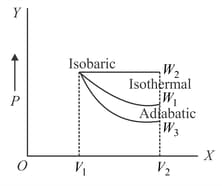
Starting with the same initial conditions, an ideal gas expands from volume$V_1$ to $V_2$ in three different ways. The work done by the gas is $W_1$ if the process is purely isothermal,$W_2$ if purely isobaric and purely adiabatic. Then

1 cm³ of water at its boiling point absorbs 540 cal of heat to become steam with a volume of 1671 cm³. If the atmospheric pressure is 1.013 x 10⁵ N/m² and the mechanical equivalent of heat = 4.19 J/cal, the energy spent in this process in overcoming intermolecular forces is

$\mathrm{\gamma }$represents the ratio of two specific heats of a gas. For a given mass of the gas, the change in internal energy when the volume expands from V to 3V at constant pressure P is

A thermodynamical system is changed from state $\left({\mathrm{P}}_1, {\mathrm{V}}_1\right)$ to $\left({\mathrm{P}}_2, {\mathrm{V}}_2\right)$ by two different processes. The quantity which will remain the same will be